|
|
| Разместил (Author): |
SergUA6  |
| Авторские права |
© http://www.radioscanner.ru |
|
|
Текст
|
Análisis de señales OFDM con SA. Espectro FFT. Segunda parte.
Vamos a tratar en mayor detalle las nuevas características del módulo OFDM en su versión 6.1.0.3
En el artículo anterior vimos como se obtenía el triángulo mágico y que su detección se producía si la señal era un OFDM con CP. También hablamos de las bases de generación de un OFDM y de la relación entre el triángulo y el símbolo LS de la señal.
Ahora vamos a fijarnos otra vez en el triángulo: Para comenzar, vamos a ver de forma esquemática como se obtiene y porqué es un triángulo. Ya dijimos que era el resultado de la correlación de dos rectángulos idénticos, pero vamos a mirarlo mas de cerca. Aquí vemos 7 pasos del cálculo de la correlación, asumiendo que LS y LG son exactos.
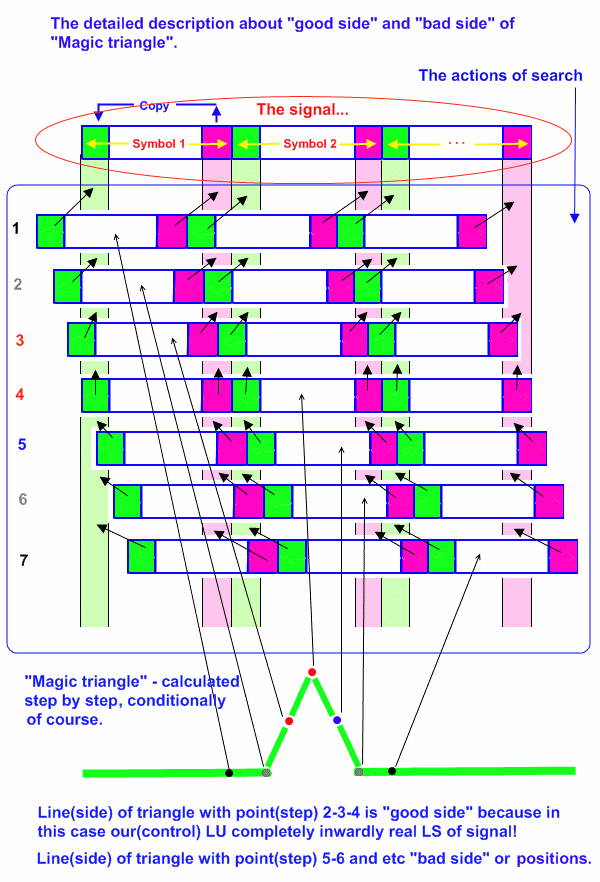
Observe que el pico del triángulo coincide exactamente con la convergencia exacta de la señal con su copia para correlación. También se ve claro que la parte izquierda del triángulo contiene toda la señal de LU dado que para formar LS se copia la parte final de LU. En la parte derecha, ya entra a formar parte de LS muestras del símbolo siguiente, por lo que LU no seria adecuado para el calculo correcto de la FFT. Pretendemos aqui que el analista sepa porqué y cómo poner la marca en el lado izquierdo del triángulo para obtener la mejor FFT posible.
Vamos a ver ahora como se forma CP (LG).
CP incrementa el número de muestras de un símbolo en una cantidad específica. Dado que CP es una copia exacta del final del símbolo, esto hace que matemáticamente esté en fase con la señal original, y por tanto la correlación entre CP y el final del símbolo sea 1. Si nos desplazamos por la señal, la correlación será 0 cuando los intervalos a correlacionar no sean CP y su origen.
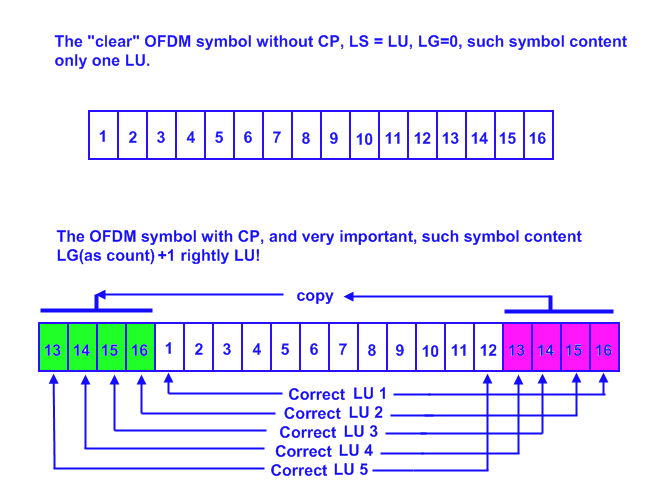
Esto es lo que nos permite una cierta libertad a la hora de seleccionar LU para la FFT, dado que si nos ponemos en el lado izquierdo del triángulo, siempre tendremos un LU completo. Esto es valido para obtener el numero de canales y sus amplitudes. A la hora de demodular la señal o ver su constelación, debe usarse el LU original,ya que hay que determinar amplitud y fase para cada símbolo.
Para dejar clara la teoría, nada mejor que generar un OFDM ideal usando OCG. Test signal .
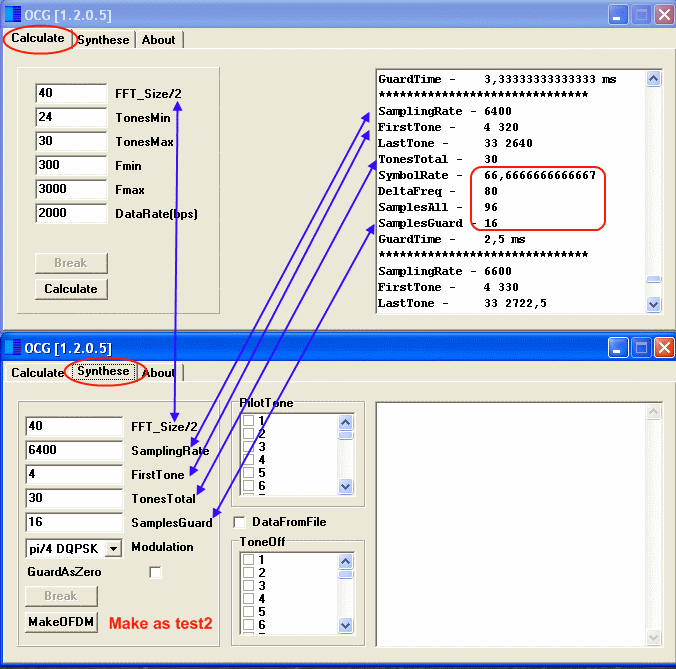
Ahora confirmamos todo lo que hemos dicho:
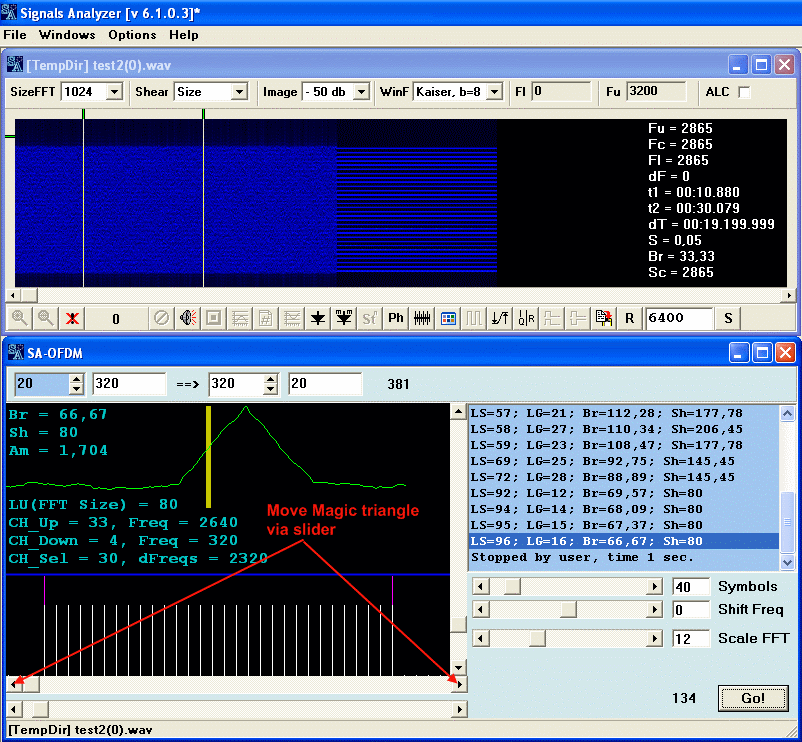
Moviendo el control indicado, puede confirmar que el lado izquierdo es el lado bueno para nuestra medida, LG y LU son correctas y la señal es estable en amplitud para los diferentes símbolos. Puede alterar el shift de la señal y ver los resultados. Si el triángulo pasa a ser negativo, aun sera buena la FFT del lado izquierdo. En general, en un OFDM, si la marca se pone en el lado no adecuado, el resultado de la FFT sera impredecible y errático.
Vamos a fijarnos en algunos detalles.
Observe que para LU =x, x es el bloque de muestras que usaremos para calcular la FFT y el tamaño de LU en el símbolo. En una señal real, x puede tomar cualquier valor. En la practica, solo tomará valores pares ya que de ser impares, debido al shift o a la frecuencia de muestreo o a ambos, LU no tendría un numero entero o par de muestras, lo que dificulta enormemente el uso del OFDM. Aún así,si se diese el caso, SA sería capaz de analizar la señal dado que el algoritmo de FFT usado admite bloques de datos impares.
Y veamos que la marca amarilla a veces es muy estrecha y otras más ancha. Esto se debe al tamaño de LS, que puede ser de valores como 20 o 2000. La imagen del triángulo se escala para adaptarla a la presentación y la anchura de la marca amarilla se escala en la misma proporción. Esto hace que si LS tiene pocos puntos, la raya sea muy ancha y viceversa.
Puede considerar que los resltados de las medidas son buenos si:
1 - el resultado es un triángulo estable para los símbolos medidos.
2 - LU es par
3 - El triángulo es positivo.
En otro caso, no habrá tanta precisión en las medidas y estas serán dudosas.
De hecho, observará que la señal OFDM es bastante tolerante a las distorsiones del canal de transmisión, por lo que se puede tener una recepción adecuada aunque aparentemente la FFT sea mala, especialmente con algunos tipos de modulación, ya que si se usa QAM, la calidad de la señal debe ser bastante mejor que si se usa QPSK, por ejemplo.
A pesar de esto, aun es posible analizar la señal y obtener sus parámetros.
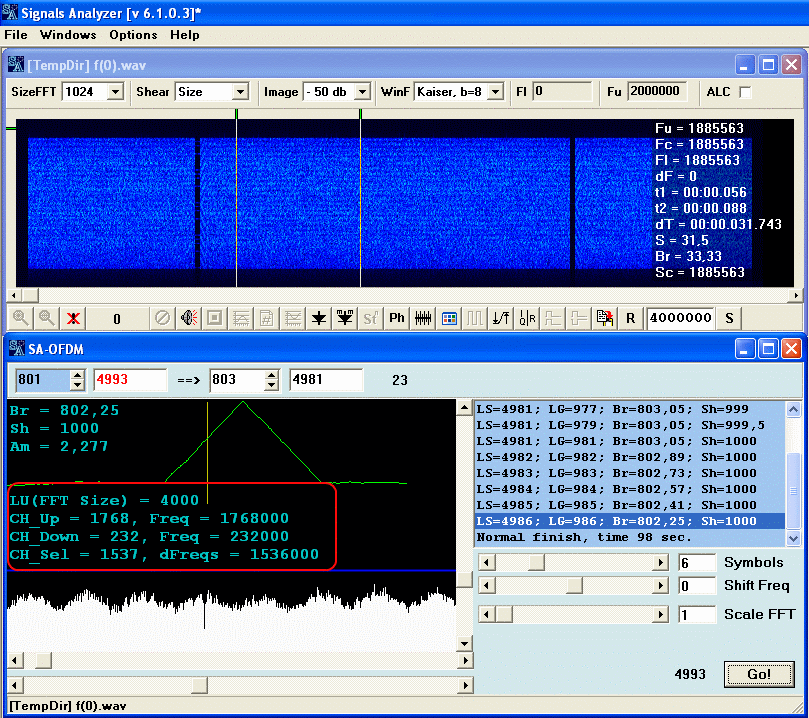
Para esta señal DAB el espectro de la FFT no cabe en la ventana de presentación. Aún así, SA le permite obtener los parámetros de la señal.
Suerte y al toro.
|
|
|
|
Добавлять комментарии могут только зарегистрированные, активировавшие регистрацию и не ограниченные в доступе участники сайта!
|
| Файл создан: 04 Nov 2009 18:20, посл. исправление: 04 Nov 2009 19:18 |
|

